1引言

共晶界面形態(tài)穩(wěn)定性是凝聚態(tài)物理學(xué)和材料科學(xué)的一個(gè)基礎(chǔ)課題[1?6].定向凝固過(guò)程中晶體形態(tài)的不穩(wěn)定性可能會(huì)導(dǎo)致不同的微觀結(jié)構(gòu)，最終極大地影響產(chǎn)品的物理和機(jī)械性能.Hele-Shaw生長(zhǎng)室是觀察共晶定向凝固過(guò)程的典型實(shí)驗(yàn)裝置，它是一個(gè)封存有樣品材料的十分扁平的容器.生長(zhǎng)室設(shè)置了一個(gè)高溫區(qū)與一個(gè)低溫區(qū)，高溫區(qū)的溫度設(shè)為TH，低溫區(qū)的溫度為TC，材料的凝固溫度TM介于兩者之間:即TC。

固體材料本身并非各向同性介質(zhì)，其晶格結(jié)構(gòu)使固體體內(nèi)的物理量以及表面的物理參數(shù)依賴于取向，變?yōu)楦飨虍愋粤?固體材料這些物理參量的各向異性特征對(duì)凝固過(guò)程動(dòng)力學(xué)與界面穩(wěn)定性機(jī)理以至對(duì)界面微結(jié)構(gòu)圖案的形成與選擇造成重要的影響[14].王志軍等[15，16]研究了各向異性表面張力對(duì)定向凝固過(guò)程中初始平界面穩(wěn)定性的影響，發(fā)現(xiàn)各向異性表面張力的非線性效應(yīng)導(dǎo)致界面傾斜生長(zhǎng).Chen等[17]研究了各向異性表面張力對(duì)定向凝固過(guò)程中球晶生長(zhǎng)的影響，發(fā)現(xiàn)在各向異性表面張力作用下，球晶生長(zhǎng)初始階段部分界面首先向內(nèi)移動(dòng)，達(dá)到一定的熔化深度后向外移動(dòng).Xu[18]研究了各向異性表面張力對(duì)定向凝固過(guò)程中枝晶生長(zhǎng)的影響，發(fā)現(xiàn)當(dāng)存在各向異性表面張力時(shí)，枝晶系統(tǒng)具有兩種不同的整體不穩(wěn)定性機(jī)理:震蕩不穩(wěn)定性與低頻不穩(wěn)定性.陳明文等[19]研究了各向異性表面張力對(duì)定向凝固過(guò)程中深胞晶生長(zhǎng)的影響，發(fā)現(xiàn)當(dāng)各向異性表面張力增大時(shí)，深胞晶界面全長(zhǎng)增大，根部低端的曲率半徑增大.本文應(yīng)用多重變量展開法研究各向異性表面張力條件下定向凝固共晶生長(zhǎng)形態(tài)穩(wěn)定性，揭示了各向異性表面張力對(duì)共晶生長(zhǎng)不穩(wěn)定性區(qū)域大小的影響.

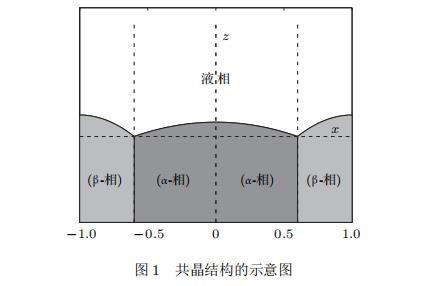
圖1共晶結(jié)構(gòu)的示意圖

2定向凝固系統(tǒng)的數(shù)學(xué)模型

假設(shè)由α和β兩相組成的片層共晶以拉度V向液相穩(wěn)定推進(jìn)，共晶片層與固-液界面垂直.選取固-液界面處α相片層的中心為坐標(biāo)原點(diǎn)，x軸與片層垂直，z軸與晶體生長(zhǎng)方向平行，如圖1所示.共晶界面用函數(shù)z=h(x，t)表示，它也是共晶生長(zhǎng)解的一部分.

本文引用Xu等[12]的無(wú)量綱化尺度，并且假設(shè)主間距的一半?w遠(yuǎn)小于溶質(zhì)擴(kuò)散長(zhǎng)度?D=κD/V，即?w??D，其中κD為溶質(zhì)擴(kuò)散系數(shù).選取?w為長(zhǎng)度尺度，V為速度尺度，?w/V為時(shí)間尺度，?H/(cPρL)為溫度尺度，Ce為濃度尺度，其中?H是單位體積內(nèi)固相潛熱，cP是比熱容，ρL是溶質(zhì)密度，Ce是共晶濃度.無(wú)量綱溫度ˉT=(T?Te)/[?H/cPρL]，無(wú)量綱濃度ˉC=(C?Ce)/Ce，無(wú)量綱無(wú)窮遠(yuǎn)處濃度ˉC∞=[(C∞)D?Ce]/Ce，其中Te是共晶溫度，(C∞)D是有量綱無(wú)窮遠(yuǎn)處濃度.為了書寫簡(jiǎn)潔起見，下文省略掉無(wú)量綱量頭上的符號(hào)“-”.各向異性表面張力用四重對(duì)稱函數(shù)γ(θ)=γ0[1+γ4cos(4θ)][14]表示，其中γ0為各向同性表面張力系數(shù)，γ4為各向異性表面張力系數(shù)，θ為界面法向量與z軸之間的夾角.共晶生長(zhǎng)系統(tǒng)還包含以下無(wú)量綱量:Peclet數(shù)Pe=?w/?D;形態(tài)參數(shù)M=(?mCe)/[?H/(cPρL)]，m是液相線系數(shù);界面穩(wěn)定性參數(shù)Γ=?c/?w，?c是毛細(xì)長(zhǎng)度，?c=γ0cPρLTe/(?H)2;無(wú)量綱溫度梯度G=(G)D?w/[?H/(cPρL)]，(G)D是與實(shí)驗(yàn)裝置相關(guān)的有量綱溫度梯度;無(wú)量綱間距參數(shù)Wc=wc/?w，wc表示α相寬度的一半.

注意到γ0，γ4，m和分離系數(shù)κ都是分段常值函數(shù)，在α相和β相都有各自對(duì)應(yīng)的常數(shù)值.用q來(lái)代表這類物理量，qα表示其在α相的函數(shù)值，qβ表示其在β相的函數(shù)值.由于溶質(zhì)擴(kuò)散長(zhǎng)度?D遠(yuǎn)小于熱擴(kuò)散長(zhǎng)度?T=κT/V，即?D??T，其中κT是熱擴(kuò)散系數(shù).界面溫度可以近似表示為TL=TS～G(z?z?)，其中TL，TS分別是液相和固相溫度，z?是與α相尖端位置有關(guān)的常數(shù).對(duì)于典型的實(shí)驗(yàn)材料，Peclet數(shù)Pe很小.以CBr4-C4Cl6[20，21]生長(zhǎng)系統(tǒng)為例，Pe≈0.01，Γ≈2.5×10?5.為了做漸近分析，本文把Peclet數(shù)Pe作為基本的小參數(shù)，假設(shè)ε=Pe?1且Γ=ε2ˉΓ，ˉΓ=O(1).

為考察共晶生長(zhǎng)形態(tài)穩(wěn)定性，利用共晶生長(zhǎng)的定常解作為基態(tài)進(jìn)行穩(wěn)定性分析.在初始時(shí)刻t=0時(shí)對(duì)基態(tài)解做一小擾動(dòng)，并將在t>0以后形成的非定常解分解成兩個(gè)部分:

其中{CB，hB}是系統(tǒng)的基態(tài)，{e C，?h}是系統(tǒng)的擾動(dòng)態(tài).假設(shè)初始擾動(dòng)態(tài)的范數(shù)共晶生長(zhǎng)系統(tǒng)的定常解為[11]:

其中

θ?是α相的接觸角，θ+是β相的接觸角，這兩個(gè)接觸角與夾度θα，θβ以及傾斜角ψ之間滿足關(guān)系式θ?=θα?π/2?ψ，θ+=θβ?π/2+ψ，如圖2所示.

將系統(tǒng)方程以振幅遠(yuǎn)小于1進(jìn)行線性化處理，結(jié)合(1)式—(4)式，可以得到共晶生長(zhǎng)系統(tǒng)的擾動(dòng)態(tài)滿足以下控制方程和邊界條件:

1)在遠(yuǎn)場(chǎng)區(qū)域，當(dāng)z→∞時(shí)，

2)在側(cè)壁x=0和x=1上，

(b)反對(duì)稱(antisymmetric)模式(A-模式)

3)在界面z=hB上，

(a)Gibbs-Thomson條件

(a)對(duì)稱(symmetric)模式(S-模式)

由三角誘導(dǎo)公式可知，

于是有

結(jié)合(9)式和(10)式，Gibbs-Thomson條件可以改寫為

(b)雜質(zhì)質(zhì)量守恒條件

3擾動(dòng)態(tài)的多重變量漸近展開解

為了得到系統(tǒng)擾動(dòng)態(tài)的漸近解，引入快變量[12]

按照多重變量(x，z，x+，z+，t+)，解可以寫成如下形式:

并對(duì)波數(shù)函數(shù)和特征值做如下展開: